What can be Done About Floating-Point Cancellation

This post talks about how what can be done about floating-point cancellation.

Scientific visualization of a very large simulation of a Rayleigh–Taylor instability problem.

One of the difficulties of dealing with floating-point arithmetic arises when subtracting numbers. When we subtract nearby quantities, the most significant digits in the operands match and cancel each other. This is called cancellation.

Example of Cancellation

Let’s look at an example. Suppose we have two quantities, a and b:

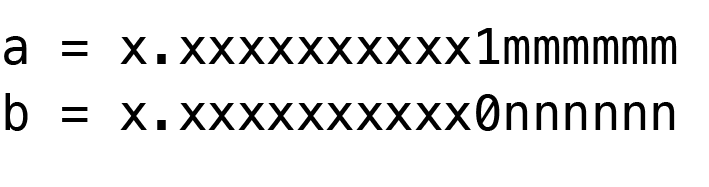
where x, m, and n are decimal digits. Suppose that due to the available precision in the system, we can only store the 12 most significant digits. As a result, when a and b are stored, the mmm… and nnn… digits are lost.

If we compute c = a – b, the result has only one significant digit:

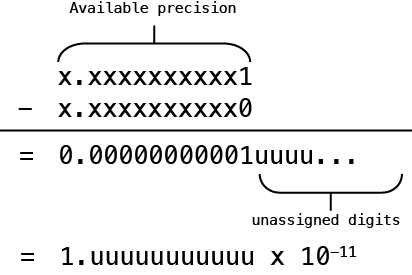
The values for the uuu… digits are not necessarily zero. Therefore, the relative error of the result can be significant. The above is an example of catastrophic cancellation, which occurs because the original quantities a and b were not represented exactly with the available precision of the system. On the other hand, suppose the a and b quantities are exactly represented as floating-point numbers in the available precision. In that case, cancellation can occur, but it is considered benign (i.e., the result of the subtraction is exact).

What Can be Done?

Avoiding cancellation can be a challenge depending on the problem being solved by the application. In some cases, rearranging the mathematical formulas can remove the problem. The paper What Every Computer Scientist Should Know About Floating-Point Arithmetic [1] gives an example of how rearranging formulas helps.

Sometimes algorithmic changes or input changes are required to avoid cancellation (see [2]). In many applications, however, it’s almost impossible to remove cancellation, and programmers must embrace it and develop a solid testing infrastructure to deal with the numerical inconsistencies and errors it may yield.

Cancellation Detection in FPChecker

Cancellation is almost inevitable in scientific applications, and it occurs very frequently. For example, many numerical methods in HPC rely on calculating differences of quantities, which often suffer from cancellation.

Because of its prevalence in scientific codes, FPChecker detects cancellation only when many digits are lost in a subtraction instruction. Therefore, FPChecker only reports cancellation when at least 10 decimal digits are lost; however, this threshold can be adjusted.

References

[1] Goldberg, David. “What every computer scientist should know about floating-point arithmetic.” ACM computing surveys (CSUR) 23, no. 1 (1991): 5-48.

[2] Lee, Sang-Hyeon. “Alleviation of cancellation problem of preconditioned Navier–Stokes equations.” Journal of Computational Physics 228, no. 14 (2009): 4970-4975.